You have probably heard about the term Big-O notation. Many companies ask about it in the interview for the software engineer position. In practice, this term is using quite rare. Becoming more experienced you will know that one solution is better than the other without using Big-O notation. If you not sure, there are profilers to help you to measure your algorithm.
Still, it is worth knowing the basics. So, in this post we will observe:
- What is Big-O notation
- Big-O complexity code examples using Javascript
- How to use Big O for algorithms complexity comparison
What is Big-O notation
Big O notation is a notation, used to describe the performance or complexity of an algorithm. It describes the limiting behavior of a function when the argument tends towards a particular value or infinity.
In programming, we need to write code using algorithms. For the same solution, we might use different algorithms. Some of them will work fast, and some will be very slow. A Big-O notation will help us to compare and choose the right solution.
Let’s see an example of notation: O(n2). Function inside brackets shows us the complexity of an algorithm. Simplified, it means that when we run this algorithm with 10 elements array size, and it will take 100 seconds to finish, when we run it 100 elements array size it will take 10000 seconds to finish.
Here is a code sample for O(n2) complexity written in Javascript.
for (i = 0; i < array.length; i++) {
for (i = 0; i < array.length; i++) {
}
}In calculations, we care only about the dominant terms. The dominant term is the term that gets biggest as n gets bigger. For example, if the function is (n2 + 2), we will use only (n2) and Big O will be O(n2). Another example: n2 + n4. In this formula, n4 will grow faster, and it will be the dominant term. Big O notation will be O(n4).
Big-O complexity code examples using Javascript
Let’s see code examples of the most common Big-O notations.
The time I am using in the examples below is not the actual time. Its main goal is to show you the difference depending on the input size, not the actual time.
O(1) complexity
function logFirstElement(array) {
console.log(array[0]);
}This notation means constant time. Whether we run this code with 1 or 1000 elements array, there will be the same 1 second.
O(log n) complexity
function binarySearch(array, target) {
let lowIndex = 0;
let highIndex = array.length - 1;
let middleIndex;
while (lowIndex <= highIndex) {
middleIndex = Math.floor((lowIndex + highIndex) / 2);
if(array[middleIndex] === target) {
return middleIndex;
}
if (target < array[middleIndex]) {
highIndex = middleIndex - 1;
} else {
lowIndex = middleIndex + 1;
}
}
return null;
}Let’s say we run this function with 100 elements size array, and it takes 2 seconds. Then if we run it with a 10000 elements size array, and it will take 4 seconds. Increasing the input size, time grows slower.
O(n) complexity
function logAllArrayElements(array) {
for (let i = 0; i < array.length; i++) {
console.log(array[i]);
}
}Let’s say we run with 100 elements size array, and it takes 100 seconds. Then if we run it with 1000 elements it will take 1000 seconds.
O(n log n) complexity
function multiDimentionalBinarySearch(arrayOfArrays, target) {
for (let i = 0; i < arrayOfArrays.length; i++) {
binarySearch(arrayOfArrays[i], target); // binarySearch from example above
}
}Let’s say we have two arrays with 100 elements each and using the function above, it will take approximately 4 seconds, 2 seconds for each binary search. Then if we run the function with 10 arrays with 100 elements each, it will take 20 seconds.
O(n2) complexity
function multiplyAllArrayElements(array) {
for (let i = 0; i < array.length; i++) {
for (let n = 0; n < array.length; n++) {
console.log(i * n);
}
}
}If we have an array with 2 elements, and it takes 4 seconds to run, then if we have 10 elements array it will take 100 seconds to finish.
O(2n) complexity
function calculateFibonacci(number)
{
if (number <= 1) {
return num;
}
return calculateFibonacci(number - 2) + calculateFibonacci(number - 1);
}If we have an array with 2 elements, and it takes 4 seconds to run, then if we have 10 elements array it will take 1024 seconds to finish.
O(n!) complexity
function iterateRecursive(inputNumber) {
for(let i = 0; i < inputNumber; i++) {
iterateRecursive(inputNumber - 1);
}
}The exclamation mark (!) here is a factorial. Factorial means to multiply all numbers decreasing input number by one. If we have an input number equals to 3, and it takes 6 seconds to run then if we run the function with an input number equals to 5 it will take 120 seconds to finish.
How to use Big O for algorithms complexity comparison
Now you know the most common algorithm complexities. Let’s say you have to choose one of two algorithms. You might calculate abstract time for both as we did above for every example and then choose the best algorithm depending on these numbers.
Or you might use the chart below to compare algorithms without sample calculations.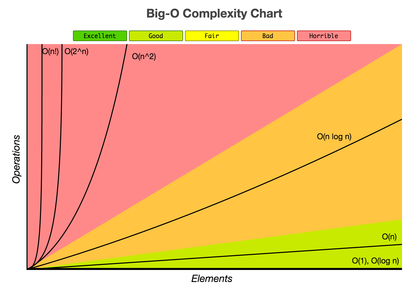
Chart from bigocheatsheet.com
Other complexity notations
Big-O notation is not the only notation used to describe algorithm complexity. Big O (O()) is mainly used, and it describes the upper bound of the complexity.
Here are some more examples or notations.
- Omega (Ω()) describes the lower bound of the complexity.
- Theta (Θ()) describes the tight bound of the complexity, i.e. upper and lower bound.
- Little O (o()) describes the upper bound excluding the exact bound.
Besides time complexity, Big O notation is used for memory complexity. Use it the same way as for the time complexity.
